Hartmann Flow

¶ HartmannFlow

Summary of the case, Hartmann Flow
Item Value/Name
Mesh Simple block mesh for a simple plate
Discritisation Governing equations: continuity equation, The Cauchy momentum equation, and the Ampère's law
Physical parameters ρ(mass density of fluid)=1 [kg/m3]
ν(kinematic viscosity)=1 [m2/s]
μ(magnetic permeability)=1 [kg⋅m⋅s-2⋅A-2, or N/A2]
σ(electric conductivity)=1 [kg-1⋅m-3⋅s3⋅A2, or S/m, or (Ωm)-1]
Initial values B(magnetic field)=(0, 20, 0) [T] and uniform
p(kinematic pressure)=(0) [m2s-2]
U(flow velocity)=(0) [m/s]
Solver mhdFoam

1. Pre-Processing

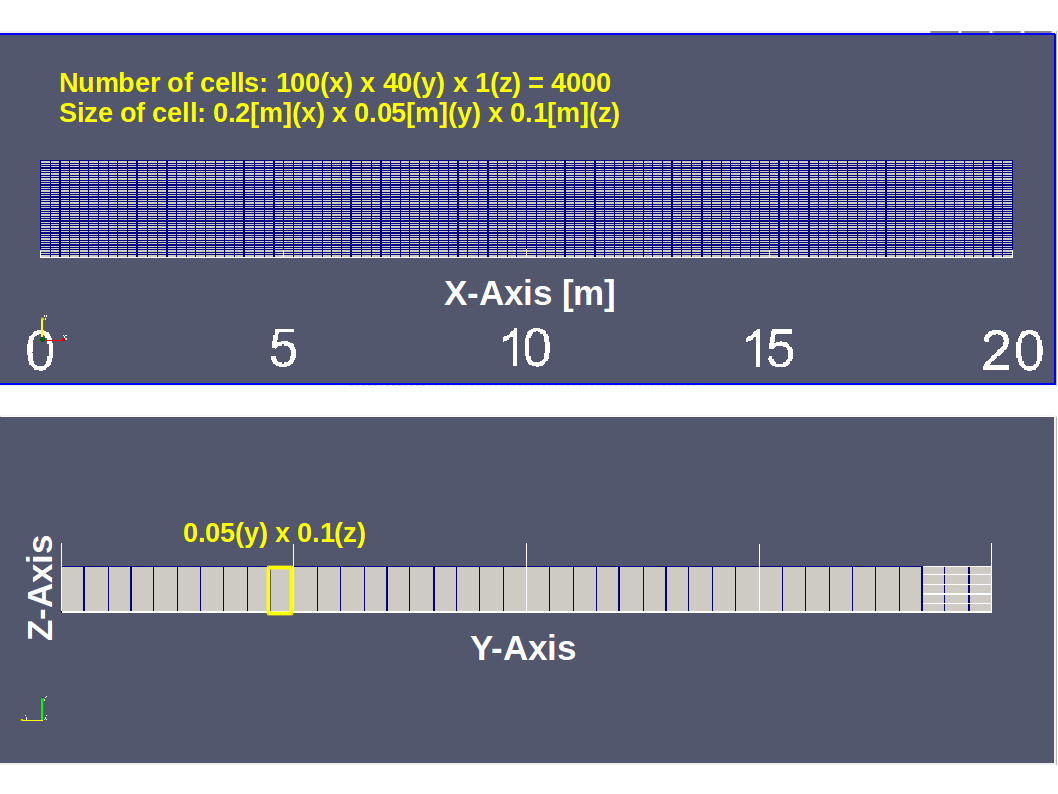
A simple plate for the Hartmann flow simulation. The size of this plate is (x:20, y:2, z:0.1)[m].
Mesh information for Hartmann Flow
Item Value
Size of one cell (x:0.2, y:0.05, z:0.1) [m]
Number of cells (x:100, y:40, z:1)

2. Settings

See the Summary of the case (above) for the physical parameters.

3. Simulation

Initial values (of pressure (p), magnetic field (B-field) and flow velocity (U) from the top) for the simulation

The following table shows the control parameters for performing a simulation.

Controll parameters for Hartmann Flow
Item Value
Start time [seconds] 0
End time [seconds] 4
Time step (Δt) [seconds] 0.005

The simulation is governed by several equations (see the Summary of the case above and the sheet below).

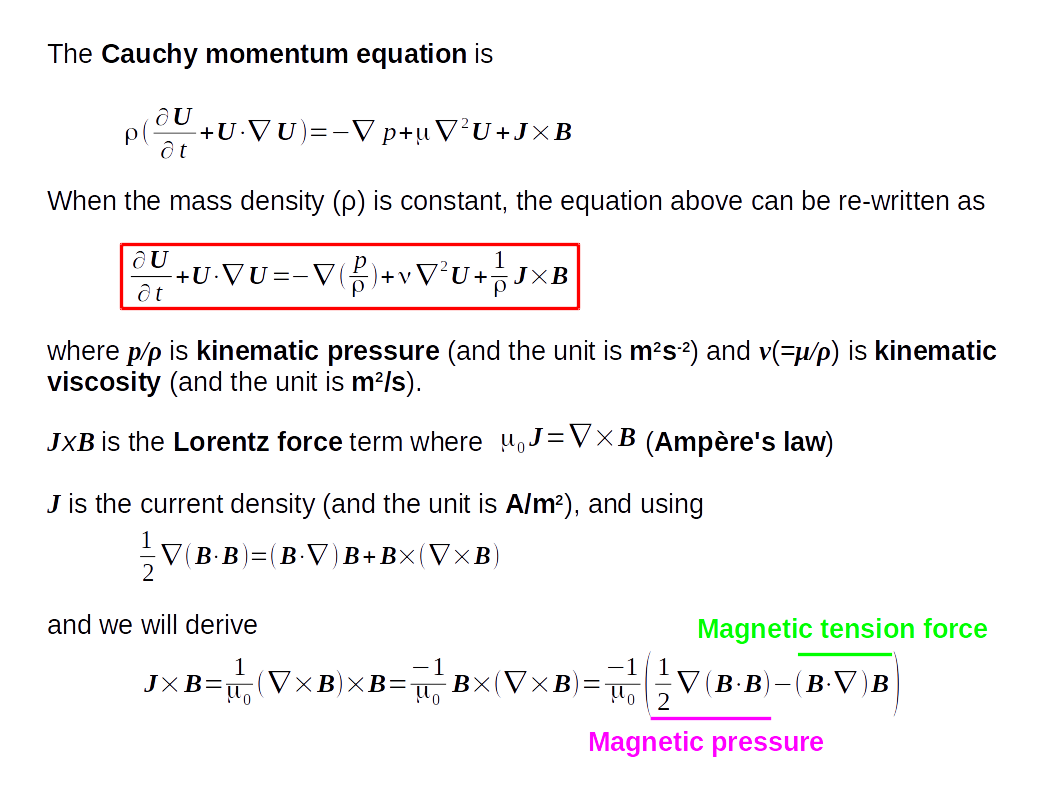
According to the sheet above, the following results on p (pressure, precisely kinematic pressure) and U (flow velocity) are the properties of fluid.

4. Post-Processing

Pressure, magnetic field and flow velocity at Time=0.5sec.
Pressure, magnetic field and flow velocity at Time=1.0sec.
Pressure, magnetic field and flow velocity at Time=1.5sec.
Pressure, magnetic field and flow velocity at Time=2.0sec.

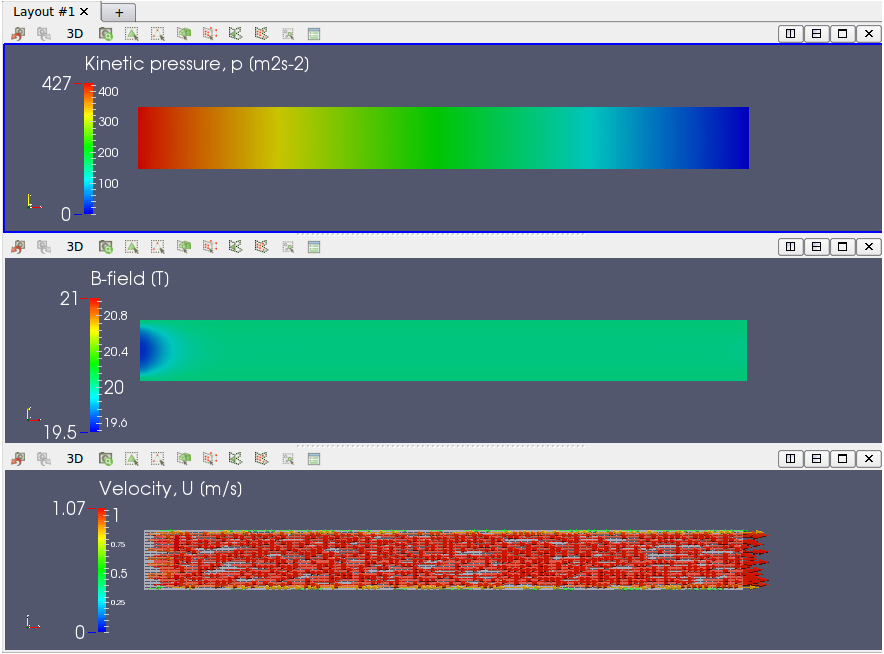
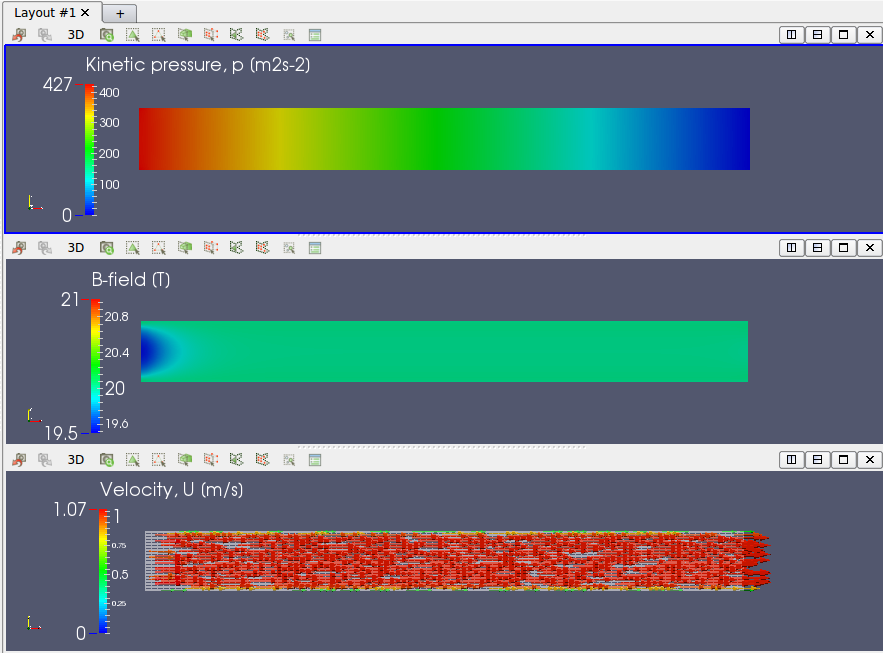
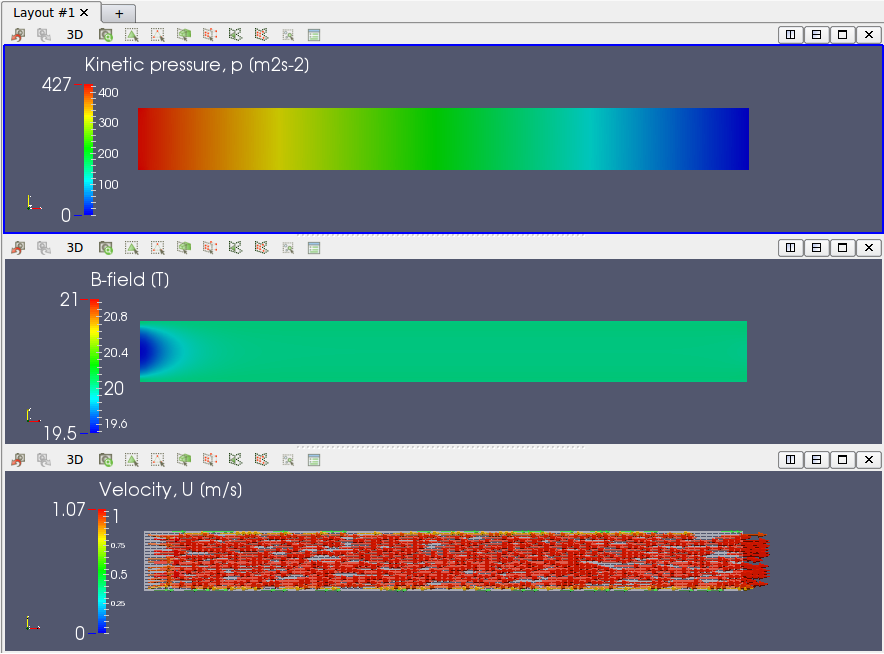
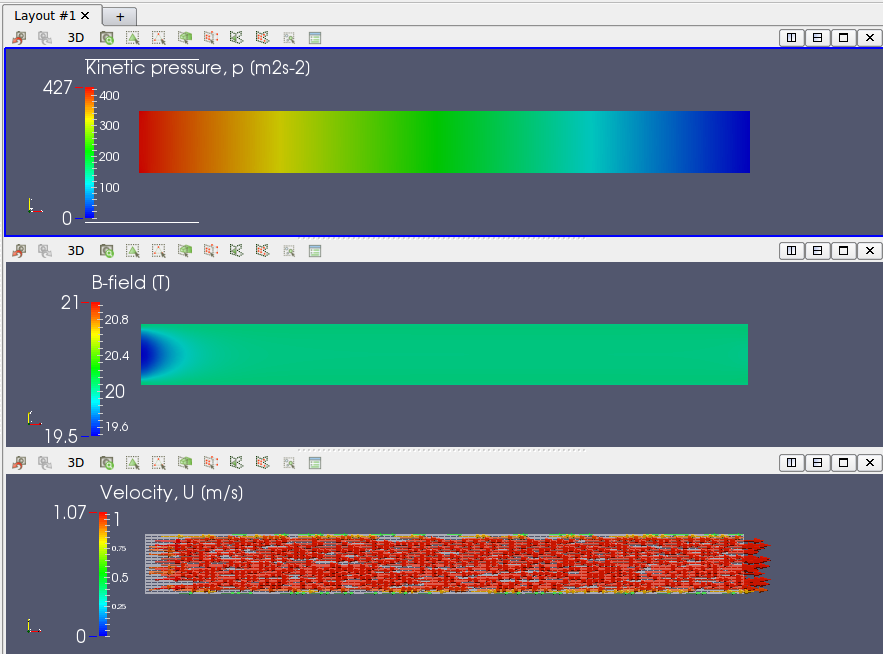
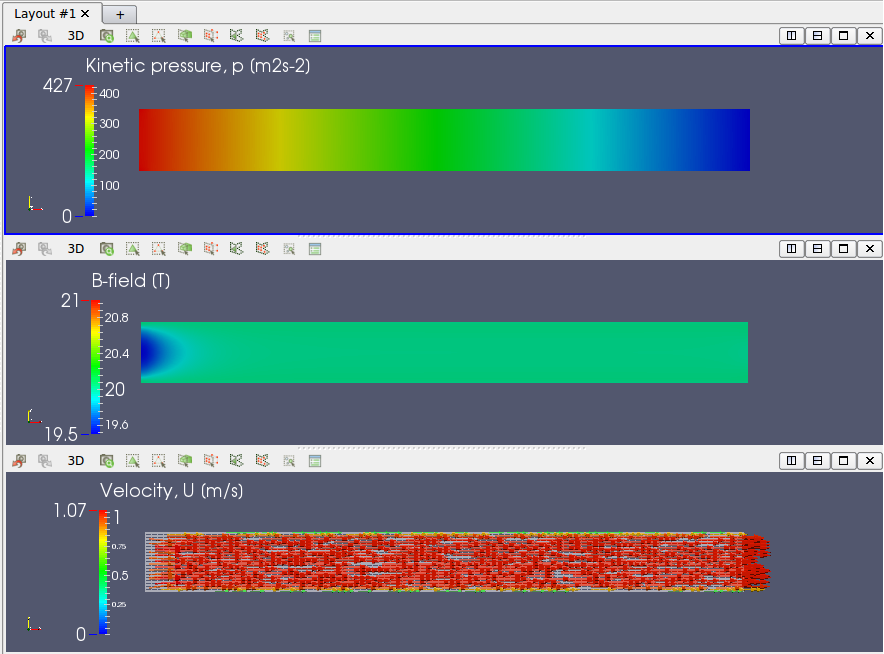
The magnetic field reaches the equilibrium state around at Time=2.0 sec.

Pressure, magnetic field and flow velocity at Time=2.5sec.

5. Analysis

In this case, most of the physical parameters are not realistic.

5.1 Hartmann Number

The ratio between fluid viscosity (ν) and magnetic viscosity (η)

5.2 Electric field applied conditions