2008-02-15 Om buckminsterfulleren
Det är några som påpekat att det inte är allmänt känt vad en buckminsterfulleren är, appropå Antons boll. För de som associerar snabbare till sportens värld än till naturvetenskapens så är strukturen den samma som en klassisk fotboll, ni vet en sån där med 12 svarta femkantiga lappar hopsydda med 20 vita sexkanter. Fysiker och mattelärare kan ju tycka att den här strukturen är intressanta av olika anledningar och eftersom jag nu faller in i båda kategorierna så kan jag ju trötta ut er en stund.
Ur fysikens synvinkel är det här en av det faschinerande kolets formationer. I skolan fick jag lära mig att rent kol finns i två former, diamant och grafit. Redan här börjar det bli kul geometri, diamant byggs upp med fyra bindningar till varje kolatom så att den bildar centrum i en tetraeder av sina fyra grannar.

Diamantstruktur, lånad från Wikimedia Commons i enligthet med GNU Free Documentation License.
Grafit däremot består av lager av kolatomer som bildar bikakemönster och ligger staplade på varandra. Om man tar ett sånt lager och drar ihop en del av sexkanterna så att de blir femkanter så stämmer ju inte mönstret längre och då måste det böja sig för att hålla ihop. Man kan tillverka såna böjda ytor och göra pyttesmå former med kolatomer som kallas fullerener. Den enklaste är, ni har redan gissat va? Buckminsterfulleren ser ut precis som Antons boll fast en miljondels mm stor.
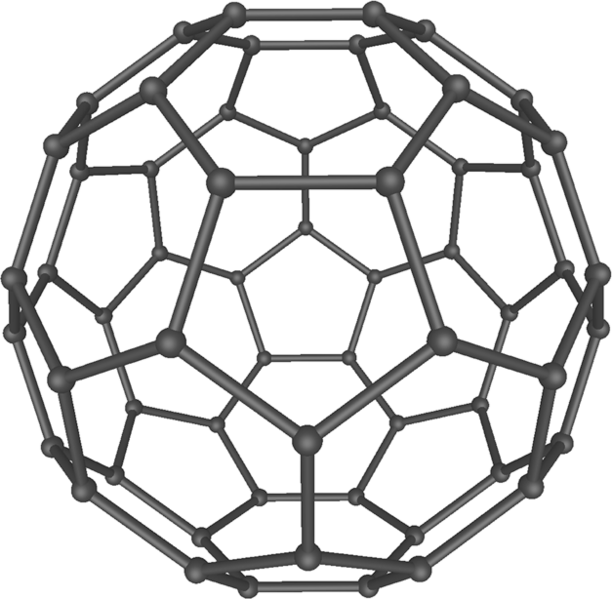
Buckminsterfulleren, lånad från Wikimedia Commons i enligthet med GNU Free Documentation License.
Ur mattelärarens synvinkel finns det fem platonska kroppar, (konvexa polyedrar med likformiga polygoner som sidor). De två största är dodekaedern som har 12 femkantiga ytor och 20 treställiga hörn (T12 för rollspelare) och ikosaedern som har 20 trekantiga ytor och 12 femställiga hörn (T20 för rollspelare).

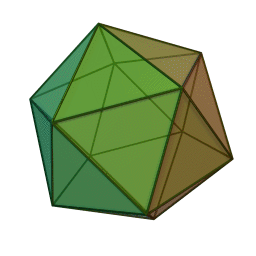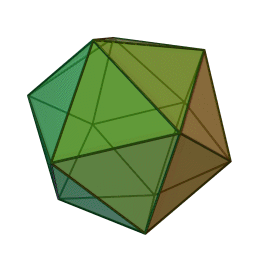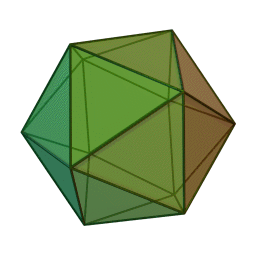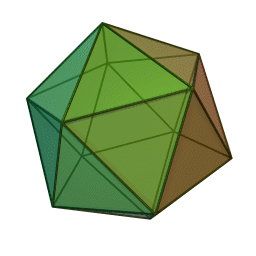
Dodekaeder och ikosaeder, lånade från Wikimedia Commons i enligthet med GNU Free Documentation License.
Är man då funtad som jag och har dessa två tärningar kan man ju inte låta bli att fråga sig om det är en slump att alla siffrorna är så lika. Det är det förstås inte, om man tänker sig att man har en 20-sidig tärning (alltså en ikosaeder) och filar av vart och ett av hörnen till en platt yta blir den femkantig. Samtidigt blir ju de ursprungliga trekantiga ytorna sexkantiga. Om man filar lagom länge så blir de till och med hexagonala. Nu känner vi igen vår kropp igen det är samma struktur som fotbollen, buckminsterfullerenen och Antons boll. Om man fortsätter och fila kommer de femkantiga ytorna man filar på att möta varandras kanter och det finns inget kvar av de ursprungliga ytorna. Då har vi fått en dodekaeder. Eftersom nu siffrorna är borta på tärningen kan vi skriva dit nya, men nu bara från 1 till 12. De här tre figurerna är alltså specialfall av en och samma struktur.
När jag kommer på såna här saker tycker jag geometri är så vackert ibland och synd om alla humanister som inte förstår att uppskatta dessa naturens små underverk. Å andra sidan har jag flera böcker av Selma Lagerlöv men det var ju bara en av dem som var bra... Så nu får väl doktorn ha mästrat färdigt. Jag lovar att jag ska skriva om något begripligt igen nästa gång.
